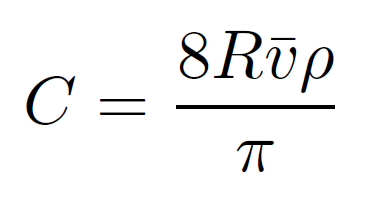Each radio button on the left-hand side controls a selection of parameters related of the model. In particular, results of simulations with different percentages of the population using the contact tracing app can be visualized through the Effect of the contact tracing app panel. The curve corresponding to the selected percentage will be highlighted in the visualization.

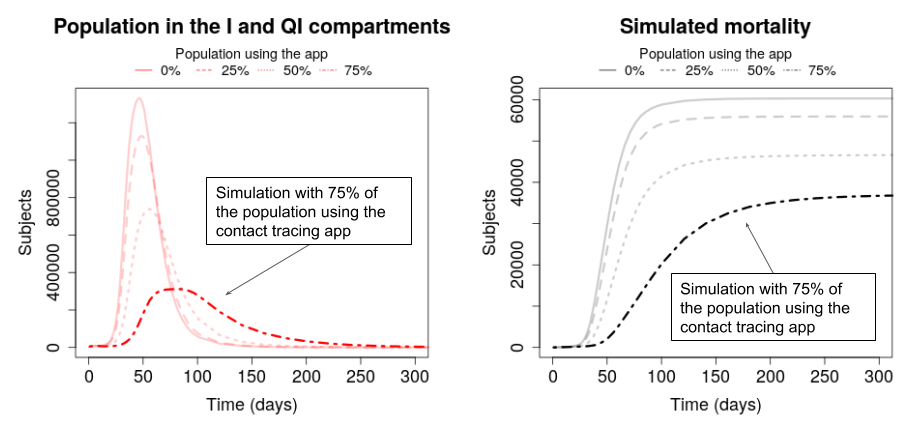
The visualization shows two plots representing the results of the simulations concerning the dynamics of the population in the I (Infectious) and QI (Quarantined Infectious) compartments (red curves on the left) as well as the dynamics of the overall mortality (black curves on the right).

The user can explore a number of illustrative scenarios by selecting combinations of parameters in the Relevant demographic and epidemiological parameters panel. This selection of parameters include:

• Population density: it can be constant (1, 5 or 20 ppl/km², reflecting small, medium and large sized cities) or variable (based on the actual Italian demography) for each node of the model.

• Contact rate: calculated based on Rhodes & Anderson (2008), it can be pre-defined (7.5, 10, or 14.8, reflecting few, medium and many contacts) or depending on a specified mobility (or velocity) (specifiy mobility).

• Mobility: it can be increased or reduced in a range (1.5, 2.5 or 5.2 km/day) based on estimations of the mobility in Spain before and after the lockdown (14/03/2020).

As described in the Model tab panel, our model takes into account many other parameters whose values are based on evidence in the literature. Nevertheless, it is important to stress that the current knowledge about SARS-CoV-2 infection and transmission is still characterized by many uncertainties. For this reason, we reckon that a user-friendly platform with relevant control options is ideal to convery the main insights of our study.

We built a Susceptible-Infectious-Recovered (SIR) model with additional asymptomatic (A) and pre-symptomatic (P) compartments and corresponding quarantine (Q*) compartments. In the following, we describe the model parameters and the bibiographic sources. The structure of the model is shown below:

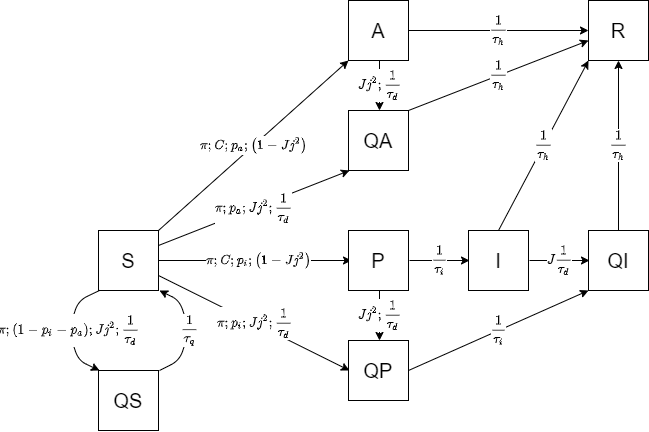
S individuals move to the A or P compartments with probabilities p_a = 0.4 [1,2] and p_i = 1 - p_a, respectively. P subjects move to I compartment after an incubation period τ_i of 5.1 days [3].

The contact tracing app recommends voluntary quarantine to people who had been in contact with a symptomatic case. As a J fraction of symptomatic cases are identified and quarantined for a period τ_q of 15 days (based on WHO recommended 14-day quarantine), Jj² is the proportion of contacts that are sucessfully contained, when a j fraction of the population uses the app and self-quarantine

The contact rate C is parametrized to a population with density ρ moving with velocity v as in Rhodes & Andreson (2008) [4], with infection transmission distance R equals to 1 meter [4]:

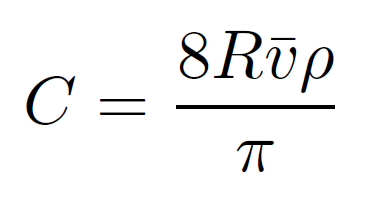
The model also includes the following additional parameters:

• A and P subjects are less infectious than S subjects by a factor f = 0.10 [1].

• P subjects are already infectious τ_d = 2 days before symptom onset [2].

• Conctact rate C is reduced by a factor q = 0.1 during quarantine.

• The probability of transmission in a single contact μ = 0.1 [1].

• The overall mortality of symptomatic cases is 1%.

[1] Ferretti et al. Science (2020). DOI: 10.1126/science.abb6936

[2] He et al. Nature medicine (2020), DOI: 10.1038/s41591-020-0869-5

[3] Lauer et al. Annals of Internal Medicine (2020). DOI: 10.7326/M20-0504

[4] Rhodes and Anderson. Mathematical Biosciences (2008). DOI: 10.1016/j.mbs.2008.08

[5] Wells. American Journal of Epidemiology (1934). DOI: 10.1093/oxfordjournals.aje.a118097

The model was developed by Alberto Ferrari (Research Foundation, Papa Giovanni XXIII Hospital, Bergamo, Italy).

The research team that contributed to the work includes:

  Enrico Santus (Bayer pharmaceuticals)

  Davide Cirillo (Barcelona Supercomputing Center)

  Miguel Ponce de León (Barcelona Supercomputing Center)

  Alfonso Valencia (Barcelona Supercomputing Center)

  Nicola Marino (Universitá di Foggia, Italy)

  Maria Teresa Ferretti (Women's Brain Project)

  Antonella Santuccione Chada (Women's Brain Project)

  Nikolaos Mavridis (Interactive Robots and Media Laboratory, IRLM)